- #1
shooride
- 36
- 0
Can one define an isomorphism/diffeomorphism map ## f: R^n\to M^m## when ##n>m##? ##M## is a non-compact Riemannian manifold..
andrewkirk said:Yes for diffeomorphism. The projection map is a diffeomorphism, eg ##f:\mathbb{R}^2\to\mathbb{R}## such that ##f((x,y))=x##.
What do you mean by isomorphism though? What is the algebraic structure that you are wanting to preserve?
If you define algebraic structures on domain and range, and find an isomorphism, it will not also be a diffeomorphism, because that would make it a homeomorphism, and there is a theorem that a n-dimensional manifold is not homeomorphic to a m-dimensional manifold if ##m\neq n##.
No, dimension is a diffeomorphism invariant. Take, e.g., the Jacobian to see why this is not possible. Dimension ( I think this is the Lebesgue dimension) is a topological, i.e., homeomorphism - invariantshooride said:Can one define an isomorphism/diffeomorphism map ## f: R^n\to M^m## when ##n>m##? ##M## is a non-compact Riemannian manifold..
Right you are. I forgot that part.WWGD said:What do you mean, isn't a diffeomorphism invertible?https://cdn.mathjax.org/mathjax/latest/fonts/HTML-CSS/TeX/png/Main/Regular/085/2212.png?rev=2.5.3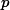












But if you're dealing with diffeomorphisms, you can use tools not available with topology alone: a diffeomorphism gives you a vector space isomorphism between tangent spaces at a point and at its image. By properties of linear maps, both dimensions are the same. OF course, a homeomorphism does not exist either, by, e.g.,as you stated, invariance of domain. You can twist this using the result that continuous bijection between compact and Hausdorff is a homeo. Consider the closed unit ball B(0,1).Then f: B(0,1)--> f(B(0,1)) is a homeo. Now consider a small open disk in B(0,1), which is sent to an open set in R^n , contradicting Invariance of Domain.lavinia said:A key theorem that answers this question is Brouwer's Invariance of Domain which says that a continuous injective image of an open set of Rn into Rn is an open subset of Rn and that the mapping is a homeomorphism. It is not hard to show as a corollary that there is not continuous injection of Rn into Rn-m m>0. A differential map is continuous so the theorem applies to differential maps as well.
BTW: This question is really a question about topology not differential geometry.
WWGD said:But if you're dealing with diffeomorphisms, you can use tools not available with topology alone: a diffeomorphism gives you a vector space isomorphism between tangent spaces at a point and at its image.
Not sure what you mean here.By properties of linear maps, both dimensions are the same. en set in R^n , contradicting Invariance of Domain.
shooride said:Can one define an isomorphism/diffeomorphism map ## f: R^n\to M^m## when ##n>m##? ##M## is a non-compact Riemannian manifold..
zinq said:Actually, any two manifolds that are topologically equivalent* must have the same dimension, so the answer here is No.
Possibly the simplest proof of this uses homology, which is a way of assigning one abelian group Hk(X) — which can at times be the trivial group {0} — to each topological space and choice of positive integer k, in such a way that topologically equivalent spaces have isomorphic groups. A mild generalization of this idea assigns an abelian group, likewise, to every pair of topological spaces (X,A) where A is a subspace of X, and every positive integer k. (This is called a relative homology group.)
Then if M and N are topologically equivalent manifolds, there must be a homeomorphism h: M —> N. This implies that for any point p of M, the relative homology groups Hk(M,M-p) and Hk(N,N-h(p)) are isomorphic.
If the dimensions dim(M) and dim(N) were not equal, let's assume, without loss of generality, that d = dim(M) > dim(N). It can be shown that for any manifold M of dimension d, the relative group Hd(M,M-p) is isomorphic to the group ℤ of integers. It can also be shown that for any manifold N with d greater than the dimension of N, the homology group Hd(N,N-q) is the trivial group {0}, where q is any point of N.
But if M and N were homeomorphic they would have isomorphic relative groups. Since they do not, this shows that any two manifolds of unequal dimensions cannot be homeomorphic.
____________
* Note: Two smooth manifolds might be "homeomorphic" (topologically equivalent) or even diffeomorphic (having a smooth homeomorphism between them, with a smooth inverse) but the word "isomorphic" is not used for topological spaces.
andrewkirk said:I would also tend to avoid purely topological explanations. While they have wider application, they can be much more abstract and conceptually demanding. If the context is Riemannian manifolds, there's no need for them.
Indeed, my current feeling is that homology theory is the most abstract topic in mathematics I have studied. I love it, but to me it seems much less intuitive than diffeomorphisms between Riemannian manifolds, which are quite visual. One of the amazing things about homology theory is that one can achieve such practical, intuitive results, using such abstract mathematical structure, and that there is at present no easier known way to achieve such results. So it's not just abstruseness for the sake of abstruseness, as some branches of mathematics sometimes appear to be.
WWGD said:I was trying to avoid (co)homology; I thought if the OP was familiar with them, s/he would not have asked the question. And I guess you could also use (c0)homology of the whole space , so that if M>N , then , if M is orientable, its highest homology, say m is, as in the case of the relative homology you used ## \mathbb Z ## , while, again as you said, the m-th homology (and anyone larger than Dim N) would be 0.
andrewkirk said:I would also tend to avoid purely topological explanations. While they have wider application, they can be much more abstract and conceptually demanding. If the context is Riemannian manifolds, there's no need for them.
Indeed, my current feeling is that homology theory is the most abstract topic in mathematics I have studied. I love it, but to me it seems much less intuitive than diffeomorphisms between Riemannian manifolds, which are quite visual. One of the amazing things about homology theory is that one can achieve such practical, intuitive results, using such abstract mathematical structure, and that there is at present no easier known way to achieve such results. So it's not just abstruseness for the sake of abstruseness, as some branches of mathematics sometimes appear to be.
But if it is not possible to do it without a Riemannian metric, it is not possible to do it with one. So the Riemannian condition is somewhat superfluous. Is there some result that an n-dimensional Riemannian manifold cannot be equivalent to an m-dimensional one that only uses properties of the metric?lavinia said:To say that there is no need for topological proofs when one is dealing with smooth manifolds ignores much of the research in mathematics that deals with the interplay between algebraic topology, differential topology, and differential geometry.
BTW: A Riemannian manifold refers to a smooth manifold together with a Riemannian metric. Your question does not involve a Riemannian metric and is not a question about Riemannian geometry. It is a question about topology. WWGD's proof uses calculus on manifolds not Riemannian geometry. It is a differential topology proof. Zinq's proof is an algebraic topology proof.
WWGD said:I guess the standard example of homeo but not diffeo is that of ## \mathbb R ## and ## (x,x^3): x \in \mathbb R ##.
zinq said:As for examples of smooth manifolds that are homeomorphic but not diffeomorphic:
The history of this is very interesting. It was not suspected that homeomorphic smooth manifolds might not always be diffeomorphic until 1956, when quite by accident John Milnor discovered that the 7-sphere S7 (the unit sphere in 8-dimensional euclidean space R8) as a topological space can be given a non-standard differentiable structure — also known as a smooth structure — for which there is no diffeomorphism with the standard S7. (In fact it turns out that there are exactly 15 distinct smooth structures on S7, where two structures are called "distinct" if there is no diffeomorphism between them.)
It is known that there is a unique smooth structure on S1, S2, S3, S5, S6, S12, S61. At present, no other-dimensional spheres are known to have a unique smooth structure — so having "exotic" smooth structures is overwhelmingly more the rule than the exception for spheres.
The most pressing problem in differential topology today is whether the 4-sphere S4 has any exotic smooth structure. Surprisingly, this has turned out to be the most difficult dimension to deal with.
But don't we need both to be diffeomorphisms to have the map from ## \mathbb R ## to itself to be a diffeomorphism?mathwonk said:WWGD, your statement in post #21, amounts to saying that projection of the graph {(x,x^3), all real x} onto the y-axis is not a diffeomorphism. Projection onto the x-axis however is a diffeomorphism.
WWGD said:But don't we need both to be diffeomorphisms to have the map from ## \mathbb R ## to itself to be a diffeomorphism?
I understand, I am aware of the existence of a unique maximal differentiable structure for the Reals, that the two structures are diffeomorphic .I was mentioning that while the differentiable structures are diffeomorphic, I believe, this map is not a diffeomorphism. This is all I meant.lavinia said:Here is a hint.
You have given the real line two differentiable structures. The first is the maximal atlas of charts compatible with the identity map - viewed as a chart.
The second is the maximal atlas of charts compatible with x -> x^1/3.
- Show that these two structures are different. This means that the two atlases are not compatible with each other.
- Show as mathwonk said that the two structures are diffeomorphic and that x -> x^3 is in fact a diffeomorpism from the first structure to the second.
EDIT: So two different differentiable structures can still be diffeomorphic. On the 7 sphere they are not only different but they are also not diffeomorphic.
mathwonk said:your post "I guess the standard example of homeo but not diffeo is that of R and (x,x3):x∈R." does not complete the words homeo and diffeo to morphic or morphism, but since you gave examples of manifolds and not maps it seems natural to assume you meant homeomorphic and not diffeomeorphic. and that is incorrect.
WWGD said:I understand, I am aware of the existence of a unique maximal differentiable structure for the Reals, that the two structures are diffeomorphic .I was mentioning that while the differentiable structures are diffeomorphic, I believe, this map is not a diffeomorphism. This is all I meant.