- #1
Joa Boaz
- 14
- 1
Two positive charges Q1 and Q2 are separated by a distance d. Find a general expression for the distance from Q1 at which the electric field is 0 by defining Q2 as alphaQ1 (alpha > 0 with alpha not equal to 1). This expression should contain alpha, d, and possible some numeric constants. Check that your expression makes sense by setting Q2 = 4Q1
I have attached the problem and what I have worked out.
 This is what I have, but unsure about it
This is what I have, but unsure about it
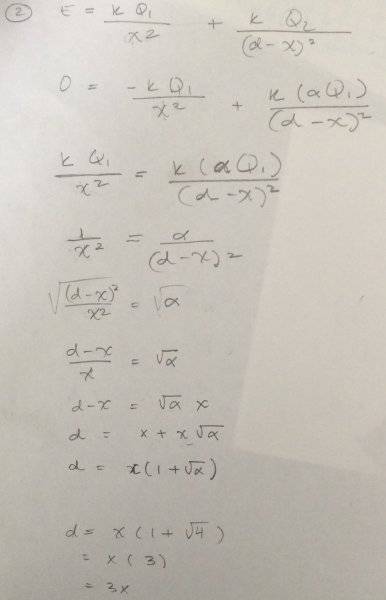
I have attached the problem and what I have worked out.