Thermodynamics Pathria Eq.4.5.9

[IcedCoffee]

I'm confused about the mathematics that led to the equation 4.5.9.

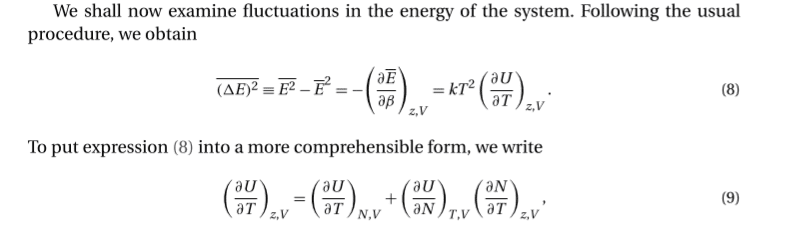
Specifically, I'm confused about what the variables that describe U are.

From the equation

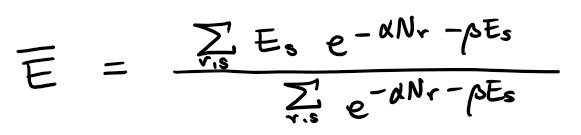
I think temperature T(through beta), chemical potential (through alpha), V (through E_s) and N (through... restriction on the summation?) defines the (average) internal energy U,

but how should I do the differentiation? What I ended up was that the chemical potential dependence can be changed to the dependence on the fugacity z so that

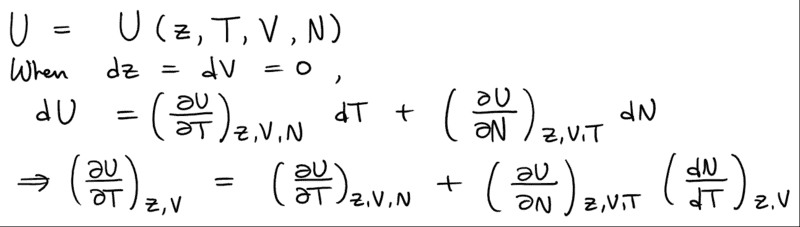
but it doesn't seem to be exactly eq.4.5.9 to me.

 

[Charles Link]

I have the answer. It's going to take me a few minutes to write out the partial derivatives in Latex... ## \\ ## ## z=z(T, N,V) ##, so that ## U(T,z,V)=U(T,N,V) ## . ## \\ ## Three parameters are need to specify ## U ##, not 4 . Any 3 of the 4, (##z,T,N,V ##), can be chosen.## \\ ## Now using the first expression for ## U ##, ## \\ ## ## dU=(\frac{\partial{U}}{\partial{T}})_{z,V} \, dT+(\frac{\partial{U}}{\partial{z}})_{V,T} \, dz+(\frac{\partial{U}}{\partial{V}})_{z,T} \, dV ##. ## \\ ## Taking the second expression: ## \\ ## ## dU=(\frac{\partial{U}}{\partial{T}})_{N,V} \, dT+(\frac{\partial{U}}{\partial{N}})_{V,T} \, dN+(\frac{\partial{U}}{\partial{V}})_{N,T} \, dV ##. ## \\ ## Now, set ## dz=0 ## and ## dV=0 ##, and set the two ## dU's ## equal. Take a partial w.r.t. ## T ## at constant ## z,V ##, (we set ## dz ## and ## dV=0 ## ), =divide through by ## dT ## everywhere, and the result is the equation 4.5.9. ## \\ ## @Chestermiller This is a good thermodynamics problem that the OP has. Might you have anything to add?

 

[Charles Link]

@IcedCoffee You have a very interesting question, but so far you haven't returned to see the answer.