Simply supported beam with a spring support in the middle - deflection

[FEAnalyst]

TL;DR Summary

How to calculate the maximum deflection of a simply supported beam with spring support in the middle when it's subjected to uniformly distributed load ?

Hi,

I'd like to calculate the maximum deflection of a simply supported beam with spring support in the middle and UDL (uniformly distributed load) acting on the whole beam:

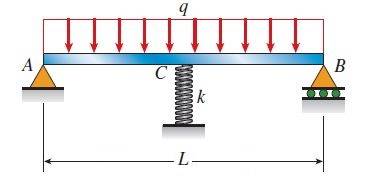
Here's my derivation, starting from the known formula for maximum deflection of a simply supported beam with UDL and no spring: $$\delta_{b}=\frac{5 \left( \frac{F}{L} \right) L^{4}}{384EI}$$ $$k_{b}=\frac{F}{\delta_{b}}=\frac{384EI}{5L^{3}}$$ $$k_{t}=k_{b}+k_{s}=\frac{384EI}{5L^{3}}+k_{s}$$ $$\delta_{t}=\frac{F}{k_{t}}=\frac{5FL^{3}}{384EI+5kL^{3}}$$

The problem is that when I substitute the data: ##F=2000 \ N##, ##L=500 \ mm##, ##E=210 \ GPa##, ##I=\frac{a^{4}}{12}=\frac{12^{4}}{12}=1728 \ mm^{4}##, ##k=100 \ \frac{N}{mm}##

the result is: $$\delta_{t}=\frac{5 \cdot 2000 \cdot 500^{3}}{384 \cdot 210000 \cdot 1728+5 \cdot 100 \cdot 500^{3}}=6.1928 \ mm$$

while from FEA, I get: ##5.1796 \ mm## and I believe this result is correct. What's wrong with my formula ?

Interestingly, I got a very good agreement for the same case with a concentrated force in the middle instead of UDL (using the same approach, just a different base formula for the deflection of the beam). Does it mean that the ##q=\frac{F}{L}## conversion is incorrect here ? How should I treat it then ?

 

[jack action]

I think this should help you figure out how to do it:

​

 

[FEAnalyst]

Well, I guess that I could use one of the standard methods to calculate the deflection of this statically indeterminate beam from scratch but I don’t know how to treat the spring. Also, the aforementioned simple approach based on the known formula for the deflection of a beam without a spring works well for the case with concentrated force in the middle so it seems that it’s just a matter of properly accounting for the UDL. Unless this simplified approach won’t work with UDL but I hope it’s not the case.

 

[Lnewqban]

The maximum deflection of that beam should be less with spring support in the middle.
The problem is that the force of the spring is proportional to that deflection.

Would this approach to a different situation be useful to yours?

https://mathalino.com/reviewer/strength-materials/problem-709-propped-beam-spring-support

 

[FEAnalyst]

Would this approach to a different situation be useful to yours?

https://mathalino.com/reviewer/strength-materials/problem-709-propped-beam-spring-support

Thank you very much. Using this approach, I get: $$\delta=\frac{5qL^{4}}{384EI}=8.9705 \ mm$$ $$\delta - \delta_{s}=\delta_{R}$$ $$8.9705- \frac{R}{k}=\frac{RL^{3}}{48EI}$$ $$8.9705- \frac{R}{100}=\frac{R \cdot 500^{3}}{48 \cdot 210000 \cdot 1728}$$ $$R=522.26 \ N$$ $$\delta_{s}=\frac{R}{k}=\frac{522.26}{100}=5.2226 \ mm$$ so pretty close to the simulation result. I also substituted everything and rearranged the equation to get a single formula: $$\delta_{s}=\frac{5qL^{4}}{384EI+8kL^{3}}$$

 

[erobz]

You should have 4 equations to work with:

$$ \uparrow^+ \sum F = R_A - wL -k y|_{x=L/2}+R_B = 0 $$

$$ \circlearrowright^+ \sum_{A} M = k y|_{x=L/2} \frac{L}{2}+ wL \frac{L}{2} - R_BL = 0 $$

Elastic Eqn's:
$$ EI \theta = \frac{R_A x^2 }{2} -\frac{w x^3}{6} + C_{\theta} \tag{slope}$$

$$ EI y = \frac{R_A x^3 }{6} -\frac{w x^4}{24} + C_{\theta}x + C_y \tag{deflection}$$

with conditions:

##y|_{x=0} = 0##

##\theta|_{x=L/2} = 0 ##

by evaluating ## y|_{x=L/2}## I believe you can combine all these to solve the system.

 

[erobz]

When I solve the system I get:

$$y_c=−\frac{5}{8}\left( \frac{wL^4}{ 48EI+kL^3} \right) \approx−5.22~ \rm{mm} $$

$$ R_A=R_B=\frac{1}{2}(ky_c+wL) \approx 738.9 ~\rm{N} $$

$$ Fc=−ky_c \approx 522.2 ~\rm{N} $$

EDIT: I found an algebra error. I see this agrees with the result in #5