Show that ##\sin(\arctan x) < x < \tan(\arcsin x)##

[Rectifier]

The problem
For ##0 < x < 1 ## . Show that
$$ \sin(\arctan x) < x < \tan(\arcsin x) $$

The attempt
I know that ## \sin x < x < \tan x ## is true for ## 0 < x < \ \pi / 2 ##

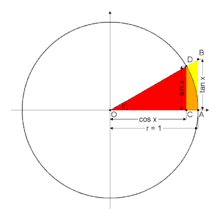x - is by definition the length DA (in radians)

I draw a right triangle with sides x and 1 and with hypotenuse ## \sqrt{x^2+1} ##

## \sin v = \frac{x}{\sqrt{x^2+1}} ##

## \tan v = \frac{x}{1} \Rightarrow v = \arctan \ x ##

## \sin (\arctan \ x) = \frac{x}{\sqrt{x^2+1}} ##I am trying to write an expression for ## \tan(\arcsin(x)) ##

## \sin v = \frac{x}{\sqrt{x^2+1}} \Rightarrow v = \arcsin \left( \frac{x}{\sqrt{x^2+1}} \right)##

## \tan v = x \Rightarrow \tan \left( \arcsin \left( \frac{x}{\sqrt{x^2+1}} \right) \right) = x##

But I fail. Please Help me write an expression for ## \tan(\arcsin(x)) ##.

 

[mfb]

I don't think this is necessary. You can compare arctan(x) and arcsin(x) with x.