- #1
mesa
Gold Member
- 695
- 38
What would be a good example of a function that would give a jump discontinuity without using piecewise or absolute values?
pwsnafu said:What do you know about Fourier series?
chiro said:You won't be able to represent a discontinuous function with any continuous function (including a Fourier series expression mentioned above)
"Bummer."
but if you want to use an analytic expression, Fourier series is a good way to do this.
The idea is that you can think of a Fourier basis like an infinite-dimensional vector space where you "project" your function on to each orthogonal basis vector (instead of having say i,j,k,... where these are geometric vectors, your basis vectors are sin(pix), cos(pix), sin(2pix), cos(2pix) etc)
Mute said:How about
[tex]y(x) = \tanh\left(\frac{1}{x}\right)?[/tex]
mesa said:So the Fourier Series basically uses 'axes' made up of trigonomic functions (i.e. sin, cos, etc. of ∏x) . They were chosen because they have an infinate number of real roots (at least without performing a transformation); it is at these orthogonal points that the Fourier series places itself.
Which part is wrong?
chiro said:It's not that: they are significant with respect to everything from geometry, to a continuous form of number theory (since they are periodic), and to the concept of using frequency to analyze things as is done in many many transforms.
"Are these things two or three dimensional?"
This Fourier decomposition is an example of an integral transform. Basically what this means is that you have an expression (i.e. a function or a signal) and you put it through this black-box and it spits out something: in this case its a number with respect to the basis vector. Then what you do is you have an inverse process which takes the results of your black-box and reconstructs the input.
There are different kinds of black-boxes and they do different things, but they all have a black-box and a reverse black-box where if you chain the reverse box after the normal box you always get back what you put in initially (provided you meet some conditions).
"So the black 'black box' is a function of trig and can be changed based on the type of problem you are trying to solve?"
As it turns out, the reason they are powerful is that they are orthogonal. Orthogonal means completely independent: kind of like if you have a vector <x,y,z> and you change y then x and z don't change at all.
"My understanding of 'orthogonal' is limited to a Calc I explanation of a point where two functions intersect each other at 90 degrees. I imagine this could be quite powerful, making a variable out of two dimensions while maintaining the other"
There are other reasons, and you can look up any kind of signal processing and pure math to find out, but the idea of taking any function over a finite interval (from -pi to pi for the default case) and then turn it into a vector (an infinite-dimensional one) is very powerful because its a standard way to take a signal and give it geometry.
The axis correspond with the trigonometric functions and the way you interpret is that the value at each axis is like the component of each vector. For example <x,y,z> have the value of x on x-axis, y on y-axis, and z on z-axis so your thinking is a good one if you think about things in terms of a vector.
If you are interested there is a whole area called Fourier analysis of which you deal with orthogonal polynomials which create vectors (like the one above) but the vectors represent something different.
So we will get numbers for a different basis, but those numbers refer to the basis of our orthogonal polynomial and not just the trig functions.
If you want to understand geometry better, then look at a linear algebra textbook to understand all this stuff for normal vectors and then you will see how this kind of thing works: you will have to learn the finite-dimensional stuff before the infinite-dimensional stuff but the ideas are the same in both.
mesa said:At what yalue of x is the jump discontinuity?
Mute said:Why don't you plot it and see?
Bohrok said:Or cot-1x.
mesa said:I asked which value of x(s) because of your question mark :)
I've been steered down the wrong path a few times so always good to get more info first, but you seem confident now, I'll monkey with it
Bohrok said:Once again, I forgot about the true graph of cot-1x
WolframAlpha likes to show the graph like this:
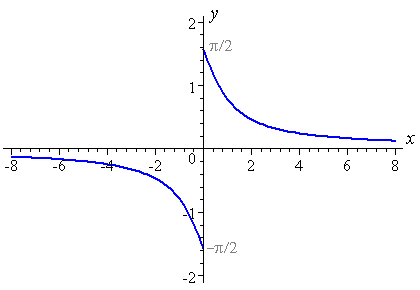
Mute said:The question mark was indicative of a suggestion using colloquial speech, as in, "Why don't you take a look at this?", rather than just saying "Look at this function." Plotting the function with wolframalpha will immediately demonstrate that the function indeed has a jump discontinuity.
I will leave it up to you to figure out why it has a jump discontinuity.
mesa said:How is it that wolfram has a completely different graph for the same function and still mean the same thing? I would guess it is changing one of the axes to be a different representation of the value, like how the sin curve is a graph of x vs y in radians as opposed to just its actual y values on the unit circle.
What's the scoop?
Mute said:The problem with y = arccot(x) is that on computer systems a one-argument version of the function cannot tell which quadrant the resulting angle y should be in. Since cot(y) = adjacent/opposite, if both the adjacent and opposite sides are negative (i.e., the angle is in quadrant 3), then the minus sign cancels out, and so typically implementations of y = arccot(adjacent/opposite) don't know that and will put angles that are supposed to be in quadrant 3 into quadrant 1. Similarly, quadrant 4 angles get sent to quadrant 2. This leads to a discontinuity in arccot(x) when this definition of the function is used.
(In case you haven't encountered it before, Tanh(x) is the hyperbolic trig function defined by
[tex]\tanh(x) = \frac{e^{x}-e^{-x}}{e^{x}+e^{-x}}.[/tex]
)
A jump discontinuity is a type of discontinuity that occurs in a function when there is a sudden, finite change in the value of the function at a specific point. This means that the function has a "jump" in its graph, where there is a gap or break between two different values.
A jump discontinuity is different from other types of discontinuities, such as removable discontinuities or infinite discontinuities, because it involves a finite change in the value of the function at a specific point. Other types of discontinuities involve the function being undefined or approaching different values from different directions.
A jump discontinuity can be caused by a variety of factors, such as a change in the domain or range of the function, a change in the sign of the function, or a change in the form of the function. These changes can result in a sudden jump in the value of the function at a specific point.
To identify a jump discontinuity in a function, we can look at the graph of the function and see if there is a gap or break in the graph at a specific point. We can also analyze the behavior of the function at that point, such as if the right-hand and left-hand limits are not equal or if the function is not defined at that point.
Yes, a function can have more than one jump discontinuity. This means that there can be multiple points in the domain of the function where there is a sudden, finite change in the value of the function. These points may be close together or far apart, and the size of the jump may vary at each point.