How can conformal mapping be used to convert curves between different maps?

[Bruno Tolentino]

I know the concepts of conformal mapping and complex mapping but I didn’t see none explanation about how apply this ideia and formula for convert a curve, or a function, between different maps.

Look this illustration…

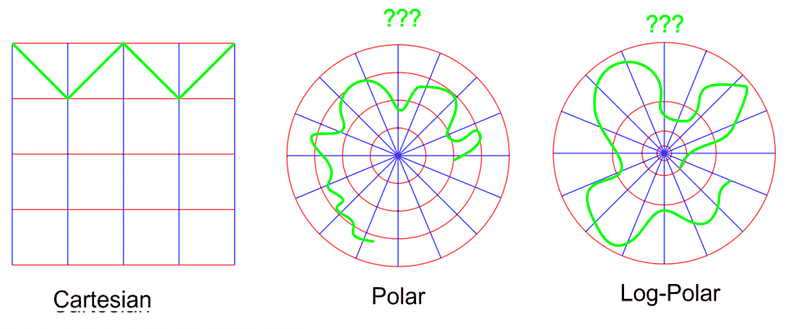
In the Cartesian map, I basically drew a liner function f(x) = ax+b (defined by part). Which would be the graph curve and the algebraic expression equivalent in the polar map and log-polar map?

 

[fresh_42]

Why don't you define ##f## properly and simply transform the coordinates?

##(x,f(x)) = (\sqrt{x^2+f(x)^2}, \arccos \frac{x}{\sqrt{x^2+f(x)^2}}) = (\log \sqrt{x^2+f(x)^2}, \arccos \frac{x}{\sqrt{x^2+f(x)^2}})##

 

[Bruno Tolentino]

Why don't you define ##f## properly and simply transform the coordinates?

##(x,f(x)) = (\sqrt{x^2+f(x)^2}, \arccos \frac{x}{\sqrt{x^2+f(x)^2}}) = (\log \sqrt{x^2+f(x)^2}, \arccos \frac{x}{\sqrt{x^2+f(x)^2}})##

Because I want (actually, I need, due the technical difficulties) to express ##r = r(\theta)##

EDIT: I can't to express an implicit funcion in polar or log polar mode...

 

[fresh_42]

Radius and angle are related by ##\cos θ = \frac{x}{r}## or ##\sin θ = \frac{f(x)}{r}## and ##r = \sqrt{x^2 + f(x)^2}.## Of course you will have to keep an eye on signs, resp. the range of the angle. In the logarithmic version in my understanding only the radius will be affected, i.e. the coordinate becomes ##\log (r)##
Maybe I didn't get what you meant.

 

[fresh_42]

EDIT: I can't to express an implicit funcion in polar or log polar mode...

You don't express functions in "polar mode", implicit or not. You can only express points in coordinates.
Therefore you write ##(x,y) = (x,f(x))## or ##(x,y) = (r(x,y), θ(x,y))##. A function expresses how a value ##y = f(x)## varies if ##x## does. The ##x-##axis is already an interpretation and a graph ##(x,f(x))## a visualization.

 

[Bruno Tolentino]

##r = \sqrt{x^2 + y^2}## ... ##(y = ax+b)##

##r = \sqrt{x^2 + (a x + b)^2}## ... ##(x = r \cos(\theta))##

##r = \sqrt{(r \cos(\theta))^2 + (a (r \cos(\theta)) + b)^2}##

https://www.wolframalpha.com/input/?i=r+=+sqrt((r+cos(t))²+++(a+r+cos(t)+++b)²)+solve+for+r

"r = sqrt((r cos(t))² + (a r cos(t) + b)²) solve for r"

solutions:

##r = - \frac{b}{a \cos(t) - \sin(t)}##

##r = - \frac{b}{a \cos(t) + \sin(t)}##

ploting:

So...

This answer is, of course, too much interesting! But, it doesn't the answer that I'm looking for...

I want that the straight of the Cartesian map becomes a curve in the polar and log polar mapping.

 

[Bruno Tolentino]

No more answers??

 

[FactChecker]

Because I want (actually, I need, due the technical difficulties) to express ##r = r(\theta)##

In general, that can not be done. There can be many r values associated with the same ##\theta## value. In the example you give, if the origin is at the center point of the first diagram, then there are entire path segments with the same ##\theta## value.

Paths should be parameterized using a separate parameter, t, in [0,1].