Help about the unit vectors for polar coordinates in terms of i and j

[srnixo]

Homework Statement

What is the significance of the negative sign [-] before [sin] in the final expression for Uθ? or was it just my mistake in the projections that prevented me from finding it?

Relevant Equations

Angular Unit Vector.

"Firstly, I represented [Uθ ]on the two-dimensional polar coordinate system to facilitate the steps and projections."

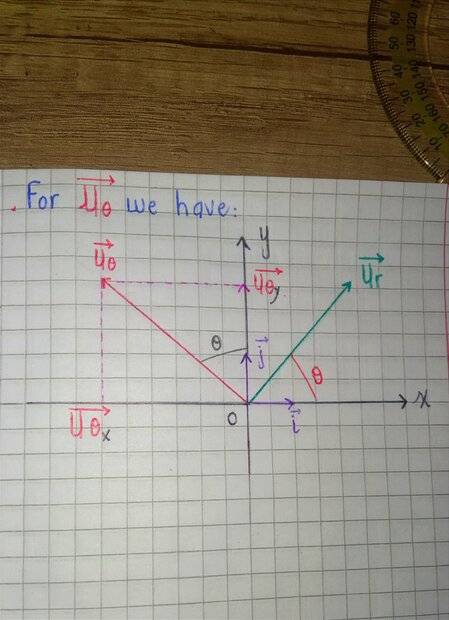
Then, I have written the steps, step by step, to ultimately derive the expression U(θ) in terms of i and j which is:
[ Uθ=−sin(θ)i+cos(θ)j ]

NOTE: The professor provided us with this expression directly, without proof, for that reason, I am aware of it. And I just wanted to substantiate it myself as an attempt."

Here are the steps:

``However, as I mentioned earlier, I did not ascertain the origin of the negative sign before sin [Uθ=−sin(θ)i] in the end . Does it merely indicate the opposite direction for the unit vector i ? (meaning it is only written as an indication in the end)? Or have I made an error in the projection concerning the angles or something like that??

I HAVE ANOTHER QUESTION: (additional)​

when i write Uθ=−sin(θ)i . Is it the same as writing Uθ=sin(θ)−i ????

Thanks for your consideration.

 

[Chestermiller]

If ##\theta=\pi/2##, what is the value of ##\sin{\theta}## and what direction is ##U_{\theta}## pointing?

 

[BvU]

Hi,

You write

First line: to decompose the vector ##\vec U_{\theta}## in two vectors ##\vec U_{\theta x}## and ##\vec U_{\theta y}##.
Second line: coefficients ##U_{\theta x}## and ##U_{\theta y}## are real numbers.

Third line I don't understand. You add ##U_\theta## (a real number ? positive definite ?) and a dot on the left side, but the right side remains the same.

Usually a dot signifies an inner product of two vectors,.

What do you mean to express here ?

[ah, Chet is faster...]

##\ ##

 

[Steve4Physics]

Your diagram seems to define ##\theta## in 2 different ways, one with respect to the x-axis and the other with respect to the y-axis. You can't do that!

Maybe this diagram makes it clearer:

(diagram taken from here: http://www.physicsbootcamp.org/Motion-in-Polar-Coordinates.html )

On the diagram, the angular unit-vector, ##\hat u_{\theta}## is directed at angle ##\frac {\pi}2 + \theta## (angle measured counter-clockwise from the +x-axis). So that's the angle you must use when finding ##\hat u_{\theta}##'s components.

when i write Uθ=−sin(θ)i . Is it the same as writing Uθ=sin(θ)−i ????

You probably meant to type: Is Uθ=−sin(θ)i the same as Uθ=sin(θ)(−i)?
The answer is yes - though it's not relevant here.

Aha. Everyone is faster than me.

 

[BvU]

Interesting ....

@srnixo , could you describe in a bit more detail what you are trying to do and precisely what alll your variables mean ? @Steve4Physics hat means he is talking about unit vectors. Are your ##\vec U## unit vectors ? From the figure I didn't conclude that ...

##\ ##

 

[srnixo]

If ##\theta=\pi/2##, what is the value of ##\sin{\theta}## and what direction is ##U_{\theta}## pointing?

When θ=π/2 the value of sin(θ)=1 because sin(2/π)=1
And after substituting that in our final expression we will get [-1]. Which means Uθ is pointing in the negative x-direction (-i).

In addition, I know that Uθ=Ur( θ=θ+2/π) which means that we obtain it by rotating Ur by an angle of π/2 in the direction of the angular rotation θ. but i'm not pretty sure if that means that: if for example Uθ is pointing in the positive x and y direction then the final expression is gonna be Uθ=sin(θ)i+cos(θ)j . In other words, that negative sign signifies only the direction of the Uθ and it is not to be directly memorized as it was!!

 

[srnixo]

@Steve4Physics :
In the illustration, the direction of Uθ doesn't matter; what's important is that it is perpendicular to Ur. which means that i can draw it like the diagram you provided or simply just like I did.
For that reason i was asking about the minus sign in the expression Uθ=−sin(θ)i if it is an indication about the direction only or a part of a general law.

 

[srnixo]

Interesting ....

@srnixo , could you describe in a bit more detail what you are trying to do and precisely what alll your variables mean ? @Steve4Physics hat means he is talking about unit vectors. Are your ##\vec U## unit vectors ? From the figure I didn't conclude that ...

##\ ##

Hello there!

Yes, i'm talking about the unit vector Uθ [polar coordinate system] and its relationship with the unit vectors i and j.
i was trying to prove the final expression from the beginning.

 

[Chestermiller]

When θ=π/2 the value of sin(θ)=1 because sin(2/π)=1
And after substituting that in our final expression we will get [-1]. Which means Uθ is pointing in the negative x-direction (-i).

In addition, I know that Uθ=Ur( θ=θ+2/π) which means that we obtain it by rotating Ur by an angle of π/2 in the direction of the angular rotation θ.but i'm not pretty sure if that means that: if for example Uθ is pointing in the positive x and y direction then the final expression is gonna be Uθ=sin(θ)i+cos(θ)j . In other words, that negative sign signifies only the direction of the Uθ and it is not to be directly memorized as it was!!

I have no idea what you are saying.

 

[Chestermiller]

@Steve4Physics :
In the illustration, the direction of Uθ doesn't matter; what's important is that it is perpendicular to Ur. which means that i can draw it like the diagram you provided or simply just like I did.
For that reason i was asking about the minus sign in the expression Uθ=−sin(θ)i if it is an indication about the direction only or a part of a general law.

It is part of the general law.

 

[srnixo]

I have no idea what you are saying.

That's what i meant it Mr.

When drawing both polar unit vectors in the x and y positive direction. The final expression of the relationship between (Ur , Uθ, i and j) is it gonna be Uθ=sin(θ)i+cos(θ)j ! Or still Uθ=-sin(θ)i+cos(θ)j (with minus sign)

 

[Steve4Physics]

@Steve4Physics :
In the illustration, the direction of Uθ doesn't matter; what's important is that it is perpendicular to Ur. which means that i can draw it like the diagram you provided or simply just like I did.

Agreed. But I provided a different drawing because (as stated) I thought your drawing made ##\theta## ambiguous. Maybe I was being too fussy.

For that reason i was asking about the minus sign in the expression Uθ=−sin(θ)i if it is an indication about the direction only or a part of a general law.

The minus sign follows from basic trig’. It’s worth understanding where it comes from and being able to derive it for yourself. Here’s one way.

If ##\hat u_r## points in direction ##\theta## then ##\hat u_{\theta}## points in direction ##\alpha = \frac {\pi}2 + \theta##.

The projection of ##\hat u_{\theta}## (length =1) onto the x-axis is
## 1*\cos \alpha = \cos (\frac {\pi}2 + \theta)##

We use the identity ##\cos (\frac {\pi}2 + \theta) \equiv -\sin \theta##. That's where the minus sign creeps in.

So the projection of ##\hat u_{\theta}## onto to the x-axis is ##-\sin(\theta)##. I.e the x-part of ##\hat u_{\theta}## is ##-\sin(\theta) \hat i##

 

[BvU]

Hello there!

Yes, i'm talking about the unit vector Uθ [polar coordinate system] and its relationship with the unit vectors i and j.
i was trying to prove the final expression from the beginning.

In that case: the decomposition of ##\vec{\hat U_\theta}## in ##x## and ##y## components can be written as$$
\vec{\hat U_\theta} =
\left (\vec{\hat U_\theta}\cdot \hat\imath \right ) {\bf \hat \imath} +
\left (\vec{\hat U_\theta}\cdot \hat\jmath \right ) {\bf \hat \jmath}
$$ and the coefficients follow from the inner procucts$$
\begin{align*}
\vec{\hat U_\theta}\cdot \hat\imath & = \left | \vec{\hat U_\theta} \right | \left | \hat \imath \right | \cos\theta_1 \\
\vec{\hat U_\theta}\cdot \hat\jmath & = \left | \vec{\hat U_\theta} \right | \left | \hat \jmath \right | \cos\theta_2
\end{align*}
$$All the | ##\ ## | are 1 and with ##\ \theta_1 \ =\ \theta_2 +\pi/2 \ =\ \theta +\pi/2\ ## you have ##\cos\theta_1 = -\sin\theta##

So that's where the minus sign comes from

[ah, duplicates Steve's post. Well, better twice than not at all]

##\ ##

 

[srnixo]

@BvU / @Steve4Physics Thank you so much . I appreciate it.