- #1
MaxJasper
- 1
- 0
Hello folks,
I am trying to find a conformal mapping transform function that maps the following region in z-plane into interior of a unit circle in w-plane:
[itex]|z-i|<\sqrt{2}\text{ ...AND... }|z+i|<\sqrt{2}[/itex]
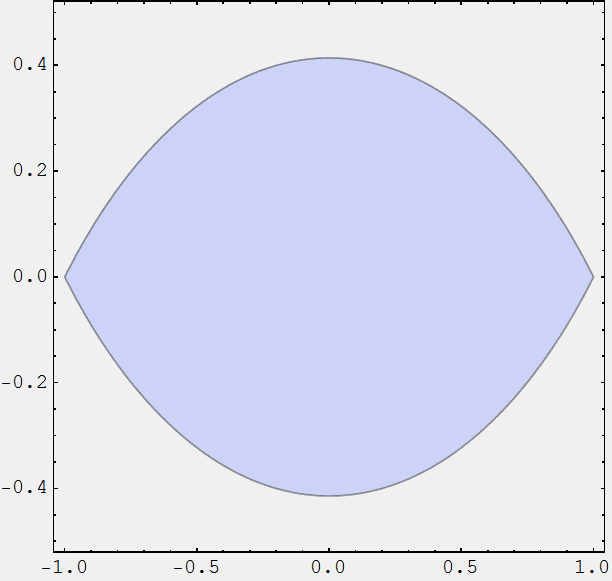
Many thanks in advance for help & clues.
Max.
I am trying to find a conformal mapping transform function that maps the following region in z-plane into interior of a unit circle in w-plane:
[itex]|z-i|<\sqrt{2}\text{ ...AND... }|z+i|<\sqrt{2}[/itex]
Many thanks in advance for help & clues.
Max.
Attachments
Last edited:
