Show that the limit (1+z/n)^n=e^z holds

[Lambda96]

Homework Statement

Show that the following applies with tasks b and c ##\lim_{n\to\infty} \Bigl( 1 + \frac{z}{n} \Bigr)^n = e^z##

Relevant Equations

Tasks b and c

Hi,

I have problems proving task d

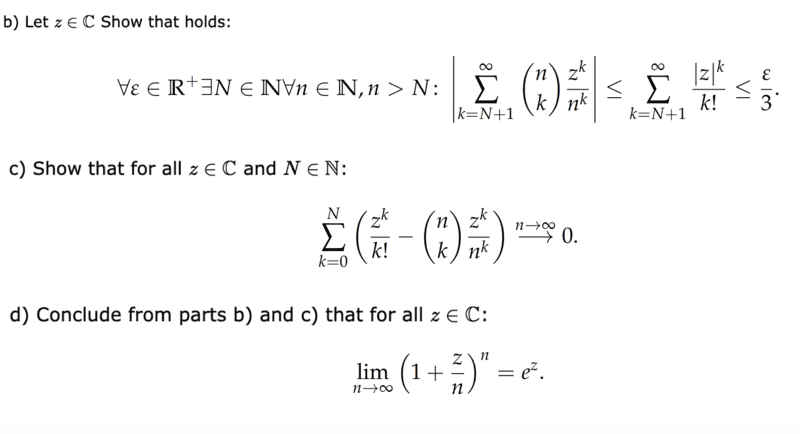
I then started with task c and rewrote it as follows ##\lim_{n\to\infty}\sum\limits_{k=0}^{N}\Bigl( \frac{z^k}{k!} - \binom{n}{k} \frac{z^k}{n^k} \Bigr)=0 \quad \rightarrow \quad \lim_{n\to\infty}\sum\limits_{k=0}^{N} \frac{z^k}{k!} = \lim_{n\to\infty}\sum\limits_{k=0}^{N} \binom{n}{k} \frac{z^k}{n^k}##

I can use the right-hand side of the equation, i.e. ##\lim_{n\to\infty}\sum\limits_{k=0}^{N} \binom{n}{k} \frac{z^k}{n^k}## with the help of the binomial theorem rewrite as follows ##\lim_{n\to\infty}\sum\limits_{k=0}^{N} \binom{n}{k} \frac{z^k}{n^k}= \lim_{n\to\infty} \Big( 1+ \frac{z}{n} \Bigr)^n ##

Now I just have to show that the left-hand side is ##\lim_{n\to\infty}\sum\limits_{k=0}^{N} \frac{z^k}{k!}=e^z##. Unfortunately, I can't get any further here, I assume that I can use task 1b for this, but unfortunately I don't know how.

 

[Orodruin]

I suggest writing out
$$
{n \choose k} = \frac{n!}{k!(n-k)!}
$$
and work from there.

 

[Lambda96]

Thank you Orodruin for your help

I can rewrite ##\binom{n}{k}## as follows ##\binom{n}{k} = \frac{n!}{k! (n-k)!}= \prod\limits_{j = 1}^{k} \frac{n+1-j}{j}## Unfortunately, I can't get any further with this either

But I'm also wondering if I'm misinterpreting the term on the left, I thought that the limit has no influence on the sum, but ##\lim_{n\to\infty}\sum\limits_{k=0}^{N} \frac{z^k}{k!}## should be ##\sum\limits_{k=0}^{\infty} \frac{z^k}{k!}##, right?

 

[Orodruin]

Thank you Orodruin for your help

I can rewrite ##\binom{n}{k}## as follows ##\binom{n}{k} = \frac{n!}{k! (n-k)!}= \prod\limits_{j = 1}^{k} \frac{n+1-j}{j}## Unfortunately, I can't get any further with this either

The last step here, while correct, is a step in the wrong direction. I suggest inserting into the expression and factorizing out the k! as that is what should appear in the expansion of the exponential.

 

[pasmith]

Consider [tex]\begin{split}
\sum_{k=0}^N \left(\frac{z^k}{k!} - \frac{n!}{(n-k)!k!}\frac{z^k}{n^k}\right) &=
\sum_{k=0}^N \frac{z^k}{k!}\left(1 - \frac{n!}{(n-k)!n^k}\right) \\ &=
\sum_{k=0}^N \frac{z^k}{k!} \left(1 - \frac{n(n-1)(n-2) \dots (n-k + 1)}{n^k}\right)
\end{split}[/tex] Note that [itex]N[/itex] is fixed, while [itex]n \to \infty[/itex].

 

[Orodruin]

But I'm also wondering if I'm misinterpreting the term on the left, I thought that the limit has no influence on the sum, but ##\lim_{n\to\infty}\sum\limits_{k=0}^{N} \frac{z^k}{k!}## should be ##\sum\limits_{k=0}^{\infty} \frac{z^k}{k!}##, right?

No, as @pasmith said, ##N## is fixed at some finite value while ##n\to \infty##. ##N## is not ##n##.

 

[Lambda96]

Thank you Orodruin and pasmith for your help

If I now calculate the limit ##\lim_{n\to\infty}## of ##\sum\limits_{n=0}^{N} \frac{z^k}{k!} \biggl( 1 - \frac{n(n-1)(n-2) \ldots (n-k+1)}{n^k} \biggr)##, the result is:

$$\lim_{n\to\infty} \sum\limits_{n=0}^{N} \frac{z^k}{k!} \biggl( 1 - \frac{n(n-1)(n-2) \ldots (n-k+1)}{n^k} \biggr)= \sum\limits_{n=0}^{N} \frac{z^k}{k!} \biggl( 1 - \lim_{n\to\infty} \frac{n(n-1)(n-2) \ldots (n-k+1)}{n^k} \biggr)=\sum\limits_{n=0}^{N} \frac{z^k}{k!} \biggl( 1 - 1 \biggr)=0$$

Unfortunately, I don't know now how to solve task d, i.e. ##\lim_{n\to\infty} \biggl( 1 + \frac{z}{n} \biggr)^n =e^z ## with the expression from task b and c