- #1
Shirish
- 244
- 32
I'm watching a nice video that tries to explain how linear algebra enters the picture in quantum physics. A quick summary:
Classical physics requires that physical quantities are single-valued and vary smoothly as they evolve in time. So a natural way to model classical physical quantities is as continuous functions. But if we try to measure energies emitted by an electron in a hydrogen atom, we see that:
1. They take only a specific set of values
2. We can't say that the energy is single-valued since prior to observation. It could be anything out of the permissible set of values
3. Each of the possible values comes up with specific probabilities
So we need a mathematical structure that accounts for all 3 of the above. The video explains it as follows:
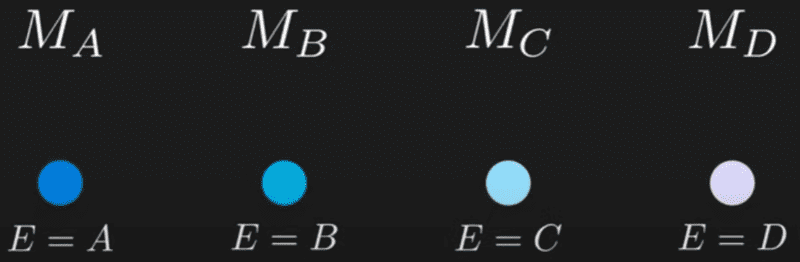
The next step is to encode the probabilities corresponding to each outcome - a natural way is to use probabilities as coefficients for these mathematical objects, which gives us ##p_AM_A \circ p_BM_B\circ p_CM_C\circ p_DM_D##. Again, a natural thing that springs to mind is linear combination - so we can try to model ##M##'s as vectors and ##\circ## as ##+##.
The paragraph above makes sense to me and I'm comfortable with the logic of deciding on the appropriate mathematical object and operation. But I'm confused about why we made the jump to a linear combination representing the particle.
From what I understand, the entire motivation was to resolve the weird behavior of physical quantities in the quantum world. So the most natural way to resolve that would've been - treat ##A,B,C,D## as vectors, and their linear combination with probability coefficients would then represent the energy. i.e. ##E=p_AA+p_BB+p_CC+p_DD##. Where and why did particles come into the picture?
[1]:
[2]: https://i.stack.imgur.com/Iezp6m.png
Classical physics requires that physical quantities are single-valued and vary smoothly as they evolve in time. So a natural way to model classical physical quantities is as continuous functions. But if we try to measure energies emitted by an electron in a hydrogen atom, we see that:
1. They take only a specific set of values
2. We can't say that the energy is single-valued since prior to observation. It could be anything out of the permissible set of values
3. Each of the possible values comes up with specific probabilities
So we need a mathematical structure that accounts for all 3 of the above. The video explains it as follows:
Let's say that we know for sure that the particle has energy ##A##, and let's say that the particle is represented by the mathematical object ##M_A## (which could be a function/element of a ring/manifold - whatever). So we have a mathematical object ##M## for every possible outcome we could get for a particle.
Somehow the particle is represented as an amalgamation of all these mathematical objects, holding on to each outcome until we make a measurement. We need to put all these objects together somehow, which can be done by some mathematical operation.
The next step is to encode the probabilities corresponding to each outcome - a natural way is to use probabilities as coefficients for these mathematical objects, which gives us ##p_AM_A \circ p_BM_B\circ p_CM_C\circ p_DM_D##. Again, a natural thing that springs to mind is linear combination - so we can try to model ##M##'s as vectors and ##\circ## as ##+##.
The paragraph above makes sense to me and I'm comfortable with the logic of deciding on the appropriate mathematical object and operation. But I'm confused about why we made the jump to a linear combination representing the particle.
From what I understand, the entire motivation was to resolve the weird behavior of physical quantities in the quantum world. So the most natural way to resolve that would've been - treat ##A,B,C,D## as vectors, and their linear combination with probability coefficients would then represent the energy. i.e. ##E=p_AA+p_BB+p_CC+p_DD##. Where and why did particles come into the picture?
[1]:
[2]: https://i.stack.imgur.com/Iezp6m.png